200以上 等比数列 一般項 2つ 282501

 等比数列の一般項がわかったところで、等比数列のよく使う性質を紹介しておきます。 それは簡単に書くと次のようになります。 等比数列の連続する3つの数 a 、 b 、 c がこの順で並んでいるとき、これらには次の関係がある。 a × c = b 2 例えば先ほど数列 数列と漸化式 数列とは 次のように数を一列に並べたもの数列（sequence of numbers）という。,,,,, (正の整数を順に並べた数列),,,,, (正の奇数を順に並べた数列),,,,, (1から3をかけ続けた数列) 1番目から数えて、第1項、第2項、第3項のように、n 番目の項を第 n 項という。一般項はnの1次式で表される。したがって、原数列の一般項は、等差数列の和を考えると、nの2次式になるだろう。 ＜まなぶ＞ 余計、分からなくなりました。 ＜先 生＞ では階差数列が等比数列の場合を考えてみよう。初項b、公比rとすると、

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列 一般項 2つ

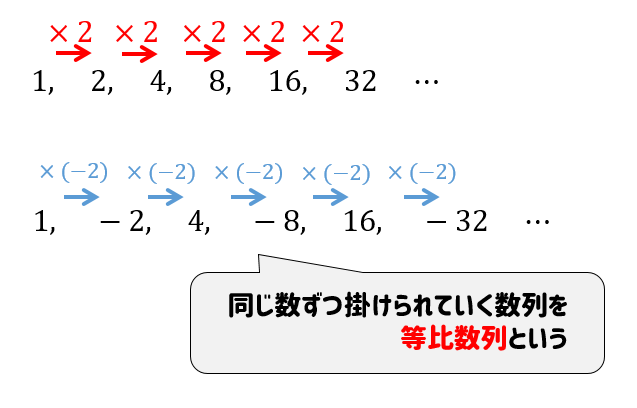
等比数列 一般項 2つ- 例題1 次の等比数列の一般項を求めよ。 ただし公比は正の実数とする。 (1) a 1 =3，a 4 =24 (2) a 3 =16 , a 4 a 5 =96 問題文に等比数列と書かれているので 初項a,公比rとおいてan=arn1まではおけます 。 あとは連立方程式を解くだけです。 答え 初項をa，公比をr等比数列を漸化式で表すと、 =, = となる。公比が負の場合は符号が一項ずつ入れ替わる数列となる。例えば 3, −6, 12, −24, という数列は公比 −2 の等比数列であり、一般項は

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

等比数列の一般項～その1～の解答 初項が2，公比が3の等比数列であり，第 n 項 (一般項)は初項 a 1 に公比 r を n − 1 回かけることによって求められるので a n = 2 ⋅ 3 n − 1 また，第10項は a 10 = 2 ⋅ 3 9 = である． 初項が81，公比が − 1 3 の等比数列だから a n = 81 ( − 1 3) n − 1 また，第10項は a 10 = 81 ( − 1 3) 9 = − 1 243 である．ポイント 等比数列の一般項 (途中からスタートOK) an = ak ⋅rn−k a n = a k ⋅ r n − k ここの k k には n n 以下の都合のいい自然数を代入できます． k = 1 k = 1 を代入したのが， an = a1 ⋅rn−1 a n = a 1 ⋅ r n − 1 になります．例えば 5 5 番目がわかっている場合は， an = a5 ⋅rn−5 a n = a 5 ⋅ r n − 5 を使えば速 先ずは，等比数列を確認しておこう． 1．集合風（列記法・外延的記法）： { \ {a_n\}\ =\ \ { a,\ ar,\ ar^2,\ \cdots \} \ (a, r定数) } 定 数 2．漸化式： { a_1=a,\ \ a_ {n1}=r \cdot a_n \ \ (n=1,2,3, \cdots) \ (a,r定数) } 定 数 3．一般項： { a_n=a \cdot r^ {n1} \ \ (n=1,2,3, \cdots) \ (a,r定

いろいろな等比数列の和 等比数列の和の公式： a ( 1 − r n) 1 − r \dfrac {a (1r^n)} {1r} 1−ra(1−rn) をいろいろな等比数列に使ってみましょう。 公比が負の数でも分数でもOK。 2 2 ( − 1 3) 2 ( − 1 3) 2 ⋯ 2 ( − 1 3) 9 22 (\dfrac {1} {3})2 (\dfrac {1} {3})^2\cdots 等比数列の一般項の公式 初項\( a_1 \)、公比\( r \)の等比数列\( \{ a_n \} \)の一般項\( a_n \)は、 \begin{align*} a_n = a_1 \cdot r^{n1} \\ \end{align*} と表すことができる。よって、求める数列の一般項は、\(a_n=3^{n1}2\cdots(解)\) 階差数列が等比数列になっている場合でも 基本的にはやり方同じ！ Σの計算方法がちょっと違ってくるだけだね。 漸化式と階差数列の問題

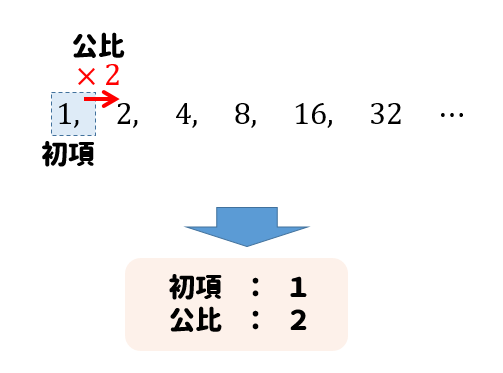
タイプ： 教科書範囲 レベル： ★★ 階差数列を用いて一般項を求める方法について解説します． 当サイトではそのような数列を階差型の数列と呼ぶことにし，深く内容を考察，解説し，演習問題まで用意しました． 目次 1： 階差型の数列 2： 一般項を 等比数列の一般項の求め方 それでは、数列を考えるのに重要な「一般項」の求め方を考えていきましょう。 まず、等比数列は次のような数列となってました。 ※ 初項が「1」、公比が「2」の例としております。性質 如果一个等比数列的首项記作 ，公比記作 ，那么该等比数列第 项 的一般項为： = 換句話說，任意一個等比数列 {} 都可以寫成 {,,,,}在一個等比數列中，給定任意兩相連項 和 （其中 ），可知公比 = 給定任意兩項 和 ，則有公比 = 這裡注意，若 是偶數，則公比可取此結果的正值或負值。

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列の和の公式は何故2個あるのでしょうか 赤で囲った2個 Yahoo 知恵袋

の形であるならば，この数列 は，初項 公比 の等比数列だから，直ちに一般項が求まります．この等比数列の第 n 項つまり一般項 a n は 「初項から第 n 項までには r を n − 1 個かける」 と考えて a n = a r n − 1 となるのはすぐにわかるだろう． また，漸化式 ( 1) から一般項 a n を求める方法もみておこう． STEP1 漸化式 ( 1) の n に 1, 2, 3, ⋯, n − 2等比数列の一般項を求める 等比数列の一般項を求める例を見てみましょう。 ここに等比数列があります。 3 , 6 , 12 , 24 , 48 この数列は「初項3、公比2の等比数列」です。 ここで等比数列の一般項の公式を思い出してみましょう。

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

この関係が成り立つ数列を 等比数列 と呼び r を 公比 と呼びます。 上の例では，初項 3，公比 2 の等比数列となります。 初項が a，公比が r である等比数列の各項は， a1=a，a2=a･r21，a3=a･r31，a4=･r41， と表現されます。 よって，一般項 an は次のように表現されます。 まとめ3 (等比数列の一般項) 初項 a, 公比 r の等比数列の一般項 an は an=a･rn1 2 等差数列とは？ 21 等差数列とは「はじめの数に、一定の数を足し続ける数列」 22 等比数列と何がちがう？ 3 等差数列の公式の意味を説明！ 31 「初項」「公差」だけを押さえれば等差数列の一般項は求められる 32 等差数列のコツ：両脇を足したら 2^2，4^2，6^2，8^2，・・・・ 簡単な数列なのですが、一般項の求め方で悩んでいます。 しらみつぶしではない解法です。 答えはan＝（2n）^2です。 等比数列だからar^n1＝anに当

等差 等比 の和 2次式 等比 の和 おいしい数学

数学b 数列 2 2 等比数列の一般項 Youtube

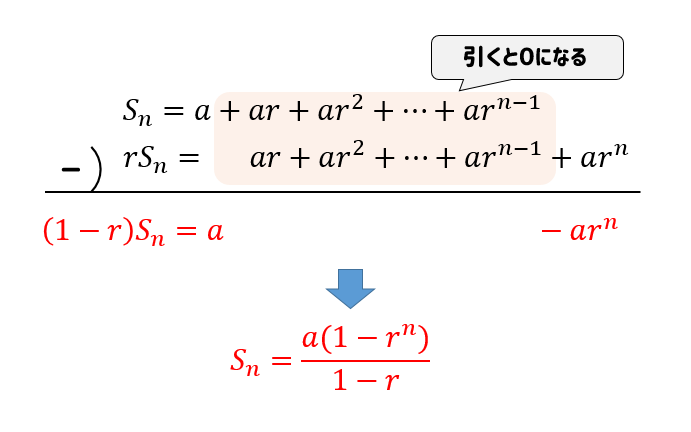
等比数列の一般項を求める公式 $$a_n=ar^{n1}$$ $$a初項 r公比$$ 等比中項 3つの項の等比数列\(a, b, c\)について、次の式が成り立つ。 $$b^2=ac$$ 等比数列の和を求める公式 \(r\neq 1\) のとき $$S_n=\frac{a(1r^n)}{1r}=\frac{a(r^n1)}{r1}$$ \(r=1\) のとき $$S_n=na$$ したがって、この数列は「初項 \(1\)、公比 \(2\) の等比数列」と表現できます。 等比数列の一般項公式 等比数列の一般項は次のように表されます。幾何数列）は、隣り合う二項の比が項番号によらず等しい数列を言う。 各項に共通する (common) その一定の比のことを公比（こうひ、英 common ratio ）という。 例えば 4, 12, 36, 108, という数列 (a n) ∞ n=1 は、各項が直前の項に 3

漸化式全パターンの解き方まとめ 難しい問題を攻略しよう 受験辞典

等比数列の和の公式で次の2つを習いました しかしこの2つの使い分けがイマ Yahoo 知恵袋

等比数列の一般項を求める 等比数列の一般項を求める例を見てみましょう。 ここに等比数列があります。 2 , 6 , 18 , 54 , 162 この数列は「初項2、公比3の等比数列」です。 ここで等比数列の一般項の公式を思い出してみましょう。初項 a ，公比 r の等比数列の一般項 a n は a n =ar n−1 （解説） 項が n あるとき，その間は n−1 個あります． a 2 =a×r 1 3．一般項： { a_n=ad (n1)\ \ (n=1,2,3, \cdots) \ (a,d定数) } 定 数 定数 d は，等差数列の公差（こうさ）という． 狭義の等差数列では， d≠0 とするが，本記事では， d=0 も含めて，広義の等差数列を扱うものとする。 （以下， a, d\in\mathbb {R} として書くが，実は

2

等比数列の一般項の問題です 解説をよろしくお願いします Clear

これにより初項が3公差が2の等差数列なので一般項は となります。 ② 等比数列型の漸化式の解き方 等比数列型の漸化式を用いる前にまずは等比数列の一般項の公式を思い出しておきましょう。 等比数列の一般項は で求めることができました。定数 係数の3項間漸化式が の形で与えられているとき， を満たす定数, を見つけると，数列 は， 初項 公比 の等比数列になるので， (I) まず2項間漸化式 の一般項を求めることができます． 1組の定数, から得られる2項間漸化式から，さらに数列 の一般練習問題2 初項が 5，第3項が ，第k項が 640 の等比数列がある。 (1) この数列の公比 r と k を求めよ。 (2) この数列の第6項 a 6 を求めよ。 (3) この数列の第3項から第9項までの和 S を求めよ。 (東北

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

等比数列とは 等比数列の意味と性質 一般項と和の公式をわかりやすく解説 Irohabook

 この最初の数を初項、加えていく数を交比といい、上の数列は、初項 2、交比 3 の等比数列であると言います。 等比数列の一般項 一般項 とは数列の第 番目が何になるかを意味するもので数列とその和 数列 何らかの規則に従って，数を一列に並べたものを数列という． 数列を記号で表わすときは，第 1 項を a 1 ，第 2 項を a 2 ，第 3 項を a 3 ，のように添字を付けて表わす． 第 n 項が a n であるような数列のことを，単に数列｛ a n ｝と書く． 例1 数列｛ a n ｝が 2，4，6，8 ここでは、等比数列に関する例題を見ていきます。数列の一部分から一般項を求める問題などを扱います。 等比数列の一部から一般項を求める 例題1 第2項が $6$ で、第4項が $24$ である等比数列 $ {a_n }$ の

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

人気の 等比数列 動画 5本 ニコニコ動画

等比数列（とうひすうれつ、英 geometric progression, geometric sequence;1．等差数列 一定の差で増える（もしくは減る） 一般項：a n =a＋(n̠̠－1)d （例）1,3,5,7,9, ‥‥ 2．等比数列 一定の比で増える（もしくは減る） 一般項：a n =ar n1 （例）2,4,8,16,32, ‥‥ 3．階差数列 前回は等差数列の練習問題を解きました。 今回から、等比数列について解説します。 等比数列とは 等差数列が、項の差が等しい数列であったのに対して、等比数列は、項の増減の比率が等しい数列のことです。 具体的には、以下のように、ある項に一定の数をかけると次の項となる数列

2

等比数列とは 等比数列の意味と性質 一般項と和の公式をわかりやすく解説 Irohabook

等比数列 数列の初項につぎつぎ一定の数を掛けて作られる数列を等比数列という。 例：2，4，8，16，32，・・・・・ 公 比 2 －125 ， 25， －5 ， 1 ， －1／5 ， 1／25 ，・・・ 公 比 －1／5 等比数列の一般項 a n ＝ a r n1 a n ＝ a r n1 a：初項、 r ：公比、 n：項数 等比数列の和 初項 a から、公比 r の等比数列の初項から第 n 項までの和を Sn とすると

漸化式の基本２ 漸化式の基本の 等差数列 と 等比数列

等差数列であることの証明 数学b 等差数列と等比数列 3 Youtube

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列の和について 数学 苦手解決q A 進研ゼミ高校講座

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

高校数学b 群数列の究極の2パターン 受験の月

等比数列の和の公式について質問です Clear

高校数学b 等比数列 A N の和 １ 映像授業のtry It トライイット

Q Tbn And9gcrhoqs Tiaw74o0thwqpqqyulvy4xv5hy7apwesqqy4i H6wzaw Usqp Cau

等比数列の一般項と和 おいしい数学

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

1

An の初項から 第n項までの和を等比数列の和の公式とシグマで求めたら答えが2つ出 Clear

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

等比数列の一般項と和 おいしい数学

3

初項2 公比3である等比数列 An において 初めて1000 Yahoo 知恵袋

等比数列

無限等比級数とは 基本からわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

等比数列をシミュレーション 図解で理解 数学入門

2 の漸化式の変形では 1 のように2つ変形を書かないのはなんでですか Clear

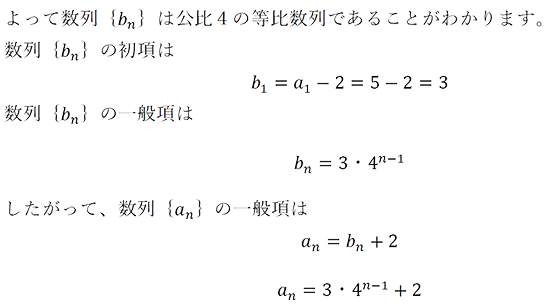
漸化式の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

等比数列の初項と公比の求め方が分かりません 教えて下さい １ Yahoo 知恵袋

等差数列に関する質問に関する質問 6ページ 勉強質問サイト

等比数列 一般項や和の計算 数学の偏差値を上げて合格を目指す

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

高校数学ｂ 漸化式 基本パターン 等差 等比 階差 特性方程式 学校よりわかりやすいサイト

高校数学b 等比数列 A N の一般項 ２ 練習編 映像授業のtry It トライイット

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

高校数学b 1つおきの漸化式 A N 2 F A N 受験の月

等比数列の和の公式で次の2つを習いました しかしこの2つの使い分けがイマ Yahoo 知恵袋

数学用語解説 数b 数列

等比数列の和の公式について質問です Clear

等比数列の和の公式の覚え方とは 問題を通してわかりやすく証明 極限についても考察 遊ぶ数学

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

等比数列とは 等比数列の意味と性質 一般項と和の公式をわかりやすく解説 Irohabook

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

無限等比級数とは 基本からわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

等比数列の和

至急お願いします 等比数列の一般項の和についてです 問題152 Yahoo 知恵袋

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

高校数学b 等比数列の一般項 A N Ar N 1 受験の月

等比数列

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

S S2 1 2 2 2 2 N 1 N2 N まで解るんですけど Clear

等比数列の公式まとめ 和 一般項の求め方をイチから学んでいこう 数スタ

等比数列とは 一般項や等比数列の和の公式 シグマの計算問題 受験辞典

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

高校数学b 等比数列 A N の一般項 ２ 練習編 映像授業のtry It トライイット

高校数学b 等比数列 A N の一般項 ２ 練習編 映像授業のtry It トライイット

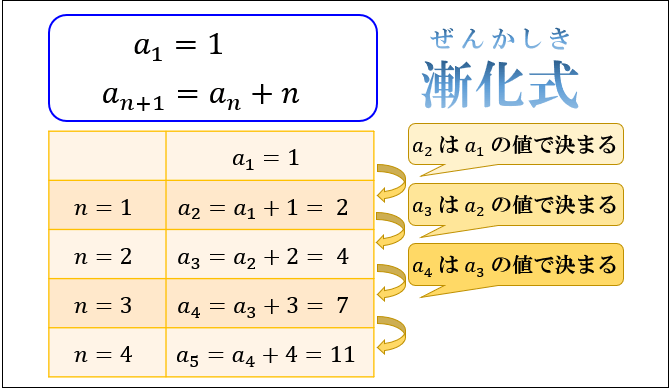
漸化式とは 等差数列 等比数列 階差数列の意味と一般項を求める公式 アタリマエ

高校数学b 等比数列 A N の一般項 ２ 練習編 映像授業のtry It トライイット

等比数列とその一般項 高校数学マスマスター 学校や塾では教えてくれない 元塾講師の思考回路の公開

等比数列の一般項と和 おいしい数学

等比数列とは 一般項の求め方や和の公式を練習問題と解説でマスターしよう 高校生向け受験応援メディア 受験のミカタ

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 21年3月15日 エキサイトニュース 6 8

高校 数学b 数列９ 等比数列の一般項２ １８分 Youtube

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

等比数列の和の公式の証明といろいろな例 高校数学の美しい物語

等比数列

等差数列 等比数列の解き方 階差数列 漸化式をスタサプ講師がわかりやすく解説 高校生なう スタディサプリ進路 高校生に関するニュースを配信

等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ

無限等比級数とは 基本からわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

この問題で B 2 を使って等比数列を考えることはわかるのですが C N は 2 8 Clear

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

高校数学b 等差数列 A N の和 １ 映像授業のtry It トライイット

2

3分でわかる 等比数列の一般項 等比中項 和の公式をわかりやすく 合格サプリ

等比数列の和の公式でｒ １のときの公式が2つありますが どう使い分 Yahoo 知恵袋

高校 数学b 数列９ 等比数列の一般項２ １８分 Youtube

無限等比級数とは 基本からわかりやすく解説 高校生向け受験応援メディア 受験のミカタ

数列は2時間で解けるようになる 外資系コンサルタントが主夫になったら

高校数学b 等比数列 A N の一般項 ２ 練習編 映像授業のtry It トライイット

高校数学b 適当に並び替えると等差数列にも等比数列にもなる3数 受験の月

高校数学b 等比数列 A N の和 １ 映像授業のtry It トライイット

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

高校数学b 等比数列 A N の和 １ 映像授業のtry It トライイット

等比数列の一般項と和 おいしい数学

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

誤答から学ぼうシリーズ 連立漸化式 ほのぼの数学頑張ろう

3

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

等比数列とは 等比数列の意味と性質 一般項と和の公式をわかりやすく解説 Irohabook

等比数列まとめ 和の公式の証明や一般項の求め方を解説 応用問題つき Studyplus スタディプラス

等差数列の公式まとめ 一般項と和の公式を分かりやすく解説

2